Lab 15: Collisions in two dimensions; Lab Partner: Jamie Lopez; 10-21-16

2) In this lab, we will accomplish to determine if momentum and energy are conserved in a two-dimensional collision.

3) Elastic collisions are both which the momentum and the kinetic energy are both conserved. The total energy system before the collision equals the total energy after the collision. If some energy were to be lost after the collision, then our definition would be inelastic collisions. Elastic collisions can also be conserved by solving it using the center-of-mass frame of reference. The frame of reference is from the perspective of the lab.

4) We will determine a lab to see if we can make an elastic collision conservative. Here we have a lab setup of 3 balls on stop on a leveled glass table. We will determine two experiments. The first will be two balls with the same mass will bounce each other off and the second of a steel ball with the greatest mass hitting a stationary ball. We will record the lab using a smartphone and modify the speed so we can determine the velocity to punch into our equation. Here is a before and after pictures of the collisions from the balls.

Marble vs Marble

Before

The moment it collides

After

Steel ball vs Marble

Before

The moment the balls collide

After

5)This is the data of two marbles with the same mass. The way we determine the velocity data from the balls was by indicating dots on both balls over time, then the software derived the equations to solve the data into velocity vs time. The boxes indicated in the graphs are the average velocity before and after the collision.
Marble vs Marble

Steel vs Marble


6) Marble vs Marble
 

Steel vs Marble


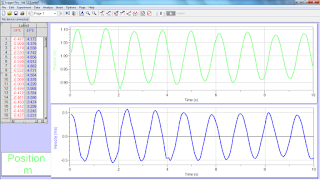
7) Marble vs Marble Graphs
On the first graph, it indicates position vs time with the two balls that collide against each other. One ball is stationary and the other ball is heading towards it. The green dots on the horizontal line indicates the ball wasn't moving before the collision. After the collision, the graph illustrates the ball moving into different directions and different speeds. The second graph illustrates the velocity of both marbles before and after the collision. The third and fourth graph illustrates the center of mass in displacement and velocity form.

Steel vs Marble
This experiment, its the steel ball heading towards a stationary marble ball. As you can see on the first graph of position vs time, the red dots indicating the steel ball still has the same rate even after the collision. This shows the heavy mass still continues towards its path even after the collision. On the velocity graph for the marble ball, it shows the marble is almost at the same speed as the steel ball.

8) After writing down the data, we wrote down the equations for kinetic energy and conservation of momentum to see if the collisions were elastic. The results were slightly similar;although they weren't exactly equal each other. This shows in the kinetic energy, energy was lost. 

Lab 14: Ballistic Pendulum; Lab Partner: Jamie Lopez; 10-21-16

2) In this experiment, we will determine the firing speed of a ball from a spring-loaded gun.

3) Before we introduce how to determine the value of the firing speed, a demonstration of the apparatus of our experiment is necessary to understand what is happening.
. We will be using a ballistic pendulum. There we have a small spring-loaded gun with the ball inside. As soon the gun fires the ball, it will make contact with a nylon block. The nylon block has a hole for the ball to enter. Behind the block is an angle indicator and the block will push the indicator as it reaches its maximum angle before it rebounds.

4) Now that we have an idea what is going on in the problem, we will determine what mechanical values are included during the ballistic pendulum problem. We know the gun is parallel to the surface of the desk so there is no angle when the ball is fired out of the gun. Next the ball makes contact with the nylon block so we will write an equation for conservation of momentum. Lastly, the ball goes vertically by some angle and returns back down. We can determine that energy was conserved by the ball and the block. The work done by the mass is the potential energy and it will equal to the change of kinetic energy.

5) Here I summarized on how to solve the firing speed of the ball.We used a weight scale for the ball and the nylon block. We next measured the length of the string. The moment the ball enters the nylon block, we will set up that point of the y-direction equal to zero. First we will solve for the velocity of the ball inside the block. At that point. Kinetic energy has a value greater than zero and the potential energy will be zero since that is the origin of y. When the mass reaches its maximum angle, the kinetic energy will be zero and the potential energy will equal to the initial kinetic energy. All we need to solve is the velocity of the ball and the block. Since the height is not vertical of the block, we know the block went up by some angle L-x. That x will equal to L cosine theta. So the height will equal L minus L cosine theta. Once we find the value of the speed of the ball and the block, we used the equation of conservation of momentum. The initial momentum will equal the mass of the ball and the unknown speed equal to the speed of the ball and block and mass. Our results came out as 4.96 +-0.677 meters per second.

6)

7) By proving that energy is conserved by the mass of the ball and the block, here is our assumption of the graph of kinetic energy and potential energy. Since the potential energy is conserved, our assumption also proves that the momentum was conserved as well.

8) In order to prove our answer of the speed of the ball is correct, we will use another method using kinematics equations. We will shoot the ball on the edge of a table, measure the values of the height and the distance where the ball lands, and use our kinematics equations to see if our assumption is true.  Substituting time for the horizontal distance and velocity in the y-component, our answer came out as 4.9+-0.32 meters per second. So our answer of the speed of the ball is correct and we proved that energy was conserved in the ballistic pendulum.

Lab 12: Conservation of Energy (Mass-Spring System); Lab Partner: Jamie Lopez; 10-21-16

2) We will be looking in a vertically-oscillating mass-spring system and accomplish that energy is conserved.

3) The work done by an object is equal to the change of kinetic energy. This is the definition of conservation of energy. If the initial quantity of energy is equal to the object's final quantity of energy, energy is conserved. There are different types of work than can be done to an object. In this experiment, we will be focusing work done by the spring and gravity.. The work done by the spring potential energy is the compression of the spring which is the displacement and the force. The work done by gravity potential energy is the vertical distance from the ground and the force of gravity. If the initial position of work done by the spring and potential energy is equal to the final position, then energy is conserved. Now the work done by the object is equal to the change of kinetic energy. So all the initial values of kinetic energy and work is equal to the final values of kinetic energy and work. The work done by all forces other than gravitational force and spring force equals the change in the total mechanical energy.

4) This is the apparatus we will use for the experiment. We will determine that the energy from its initial position will equal to the energy at its final position. The system will be oscillating so our graphs will show a sine function until the motion sensor ends the session of the object's movement. At the initial point where the spring is unstretched of 0.97 meters above the motion sensor, which is on the ground, the elastic potential energy should be zero, gravitational potential energy will be greater than zero, and the kinetic energy will be zero since the object hasn't moved yet. We will determine the y-direction going down will be positive.

5) These are the data points that the software of loggerpro recorded in the experiment. According to the values of the data record, our assumption of the graph will be a sine function since the numerical values oscillate from positive to negative.

6)

7) The first graph of the Force vs position of stretch, the values oscillate because the force is constantly stretched and pulled. Since the graphs demonstrate a repeating value over time, it proves that energy is conserved by the energy of kinetic, elastic, and gravitational potential energy. If another work disturbed the net system, the graph would demonstrate a decreasing slope at that given time.

Lab 13: Magnetic Potential Lab, Lab Partner: Jamie Lopez 10-20-16

2) In this experiment, we will approach to prove that energy within an object can be conserved.

3) The total work done on a body by external forces is related to the object's displacement, which is the change in position. The total work is also related to the speed of the object which is called Kinetic Energy (KE). If gravity is the only force that acts up on an object during a free fall, then we call this work Gravitation Potential Energy (GPE). So if the total kinetic energy is equal to the total work done by gravity, then the total energy is equal to the change in kinetic energy plus the change in potential energy. This total energy is also called total mechanical energy of the system. Energy is conserved if only no other external force interacts with the object.

4) This is what we'll do in this experiment. We will convert the cart's kinetic energy to potential energy and prove that energy is conserved. However, the cart will not be in free fall or experiencing gravitational potential energy during the test. We will use another similar approach which is magnetic potential energy. A friction-less cart with a strong magnet on one end approaches a fixed magnet of the same polarity. When the cart's position approaches to the fixed magnet, its' kinetic energy will be zero at that point while the energy is converted to magnetic potential energy. Then right after, the cart bounds back and magnetic energy is converted back to kinetic. We don't know the relationship in magnetic potential energy like we do in gravitational potential energy. So our job is to find an equation for it, and prove that the system is conserved. First we will find the distance, which we'll call r, of between the same polarity of the magnet. The distance the magnets are pushing each other will be the force. The relationship for work is force and distance. We will incline the ramp the cart is on with no friction, and let gravity do its work when the magnets repel each other. The higher or more inclined the ramp is, the closer r becomes.

5) Here is the data we recorded while finding r using a caliper and the angle respect to the flat surface using an android application.  Using these data points, we punched these values in a graph and the result gave us the equation for force.. Since the graph isn't a linear equation, we will have to integrate the equation to find the work done.. So U(r) is the equation for the work done for magnetic potential energy.

6) Now we will graph the results when the cart goes through the conservation of energy system.

7) We did experience technical difficulties during the experiment; however, we got the results we wanted. The first graph, which is Position vs time, shows the cart approaching to the motion sensor and then rebounds at the one second. The kinetic and magnetic potential energy vs time graph are equal but opposite to each other. This is what we wanted in our results.

8) In the velocity vs time graph, the object's speed begins to decline and reaches zero at one second. Since kinetic energy involves with speed, it makes sense the kinetic energy declines to zero to the 1 second interval. As the object gets closer to the origin at 1 second, the r value increases in the magnetic energy function and after the rebound r begins to increase. The reason why the object rebounds is because same polarity of two magnets repel. Since the graph looks symmetrical during the one second interval rebound, energy is conserved. If energy wasn't conserved, then the right end of the graph at the one second interval would be asymmetric.

Lab 11: Work-Kinetic Energy Theorem; Lab Partner: Jamie Lopez; 10-14-16

2) In these two experiments of Work-Kinetic Energy Theorem, we will measure the work done when an object attached to a spring stretched goes through a measured distance and how the work done by the spring is related to the kinetic energy of the object.

3) First we will begin the experiment of what Work is. Work is a quantity measurement of how far an object travels from an external force. It is the product of the force magnitude F and the displacement s or x.  The unit of work is measured in Joules (J) or N*m.  In order to graph this to get an intuitive understanding, let's demonstrate Force vs Displacement graph and how it equals to work.
The shaded region under the equation is the quantity of Work done by an object.

4) In our experiment, our apparatus will be set up with a ramp, cart, motion detector, force probe, and a spring. The spring will be our force apparatus to find how much work is done while the cart moves from its' initial position to its' final position. The force probe sensor attached between the spring and the cart will give our software a reading of how much force was used over a distant interval. The motion detector reads the object's movement of how far or close the object is.

5) For a better understanding of our data point, imagine the force vs displacement graph is similar to y vs x graph. The graph represents a linear equation of y=mx+b. The slope of the graph is the spring constant from our spring apparatus. The data shows the slope is 8.108N/m. The y-intercept should be zero and is close to zero, but of course, due to human error of our response time when the test experiment starts, the y-intercept is 0.05671N. Here is another demonstration why the spring constant graph is a linear slope. 

6)

7) The pink shaded region under the graph is the area of work done to the cart. The work done to the object from the spring is 0.8191 J or N*m. Another way to find work done to the cart is integrating the force and the distance. .

8) Our prediction of finding work done to the object is 0.8209 J or N*m. Our prediction was pretty close of finding Work comparing to the results the software read. Our percentage error is off by 1 percent, so its pretty close.

9) On the next experiment, we will demonstrate how the work done is related to the change of kinetic energy. Kinetic energy is a scalar quantity, it depends on the particle's mass and speed. We convert the force that is applied on the object to mass and acceleration. Here is the conversion using kinematic equations and assuming acceleration is constant.

So with the formula provided, we will prove the work done on the cart will be equal to the change of kinetic energy.

10) We used the same apparatus to in this experiment except our initial position of the cart will be close to the motion sensor with the spring stretched 0.6 meters. When we let go of the cart, the kinetic energy will be greater than zero because the force of the spring is pulling back to its' equilibrium state. After the spring reaches equilibrium state, it will then become compress and the force will now push the cart to the opposite of its direction.

11) According to the data, here is what our assumption our results will be. 
The area of work done will be equal to the change of kinetic energy.

12) After recording our experiment, the graph represents the work done to the cart and the kinetic energy during the object's movement. We chose an area between the points to see if it matches our calculations. Our initial position will start at 0 meters and final position will be 0.379 meters. The spring constant is still the same value according to the past experiment.

13) Our assumption came close to the answer we received. The kinetic energy the lab read is 0.675 Joules. Our spring constant was suppose to be 8.108 N/m. Perhaps a human error was caused during the test but still pretty close. After all, our experiment proves how the work done to an object is related to the change of kinetic energy.